The use of SCPT and HVSR for site period and subsoil class estimation

ABSTRACT

NZS 1170.5:2004 provides a subsoil classification system of classes A to E, which are determined by specific criteria of soil or rock characteristics. The fundamental site period, T, is a key parameter in the classification system and is particularly useful in deciding between soil classes C and D, where the boundary is T = 0.6 s. The site period can be estimated from a shear wave velocity profile, such as that obtained from a downhole seismic test. The seismic cone penetration test (SCPT) provides a rapid means of obtaining shear wave velocity without having to drill a borehole. In addition, to the downhole seismic (S) part of the test, the CPT component can also provide an independent estimate of Vs by way
of empirical correlations. The horizontal to vertical spectral ratio (HVSR) is a non-intrusive method of collecting and assessing ambient seismic vibrations that can be used to estimate the fundamental site period directly.

This paper describes how SCPT and HVSR techniques can be used separately or in combination to estimate site period and subsoil class for soil sites. Methods for interpolating SCPT data and extrapolating beyond the depth of the tests are also discussed. The methods are illustrated by a case example from a site in Auckland in Puketoka Formation soils.

1 INTRODUCTION

The New Zealand earthquake loadings standard (NZS 1170.5:2004) provides a subsoil classification system, which categorises sites into five classes, A to E. Classes A and B represent rock sites and are relatively easy to identify, whereas determining the soil classes, C to E, can be more difficult. In simple terms, Class E is defined as sites where there is 10 m or more of soil with shear wave velocity, Vs, of less than 150 m/s. If not Class E, then Classes C and D are distinguished by the fundamental site period, T; Class C if T < 0.6 s and Class D, if T > 0.6 s. There are other alternative criteria that relate to borehole information.

NZS 1170.5 specifies a hierarchy of methods for site subsoil classification, as follows:

1. From the site period based on four times the travel time of shear waves from the underlying rock to the ground surface
2=. From borelogs, including measurement of geotechnical properties (undrained shear strength, su or SPT N)
2=. From site period determined from Nakamura ratios (HVSR)
2=. From site period determined from recorded earthquake motions
3. From boreholes with descriptors but no geotechnical measurements
4. From surface geology

The hierarchy would suggest the intent of the Standard is that some form of determination of site period is the preference. Although, classification from borelogs with geotechnical properties is ranked second equal in the hierarchy, such borehole information cannot reliably quantify site period. In boreholes, the geotechnical properties that are mentioned in the Standard (su and SPT N values) are typically determined by handheld shear vane or SPT tests taken between drill runs (usually 1.5m). These tests have a high degree of uncertainty associated with them and the large depth interval between tests provides sparse, non-continuous information with depth. Furthermore, correlations between su or SPT N with shear wave velocity or site period are generally poor and difficult to verify on a site-specific basis. In comparison, CPT provides more reliable data in a near continuous fashion and correlations from CPT to Vs can be site-specifically verified if done in conjunction with downhole seismic testing (i.e. SCPT).

In the authors’ opinion the hierarchy of testing, in alignment with the believed intent of NZS 1170.5, would more aptly be:

1. Site period determined from in situ shear wave velocity testing (e.g. SCPT)
2. Site period determined from HVSR
3. Site period determined from CPT correlations to Vs (using verified correlations)

Boreholes, either with or without su and SPT N information, would sit well below these three methods in the hierarchy. NZS 1170.5 has presumably included methods for estimating subsoil class from borehole information because better methods were not previously readily available. Given the now widespread availability of in situ shear wave velocity testing, it is difficult to see how the use of borehole information can be justified for this type of assessment. Larkin and van Houtte (2014) found that applying borehole information to Table 3.2 of NZS 1170.5, which helps identify class C sites, and clause 3.1.3.7, which deals with layered sites, provides inconsistences and may result in the unconservative selection of subsoil class. Consequently, Larkin and van Houtte (2014) recommended that Table 3.2 be either amended or removed from future iterations of the Standard. It is the authors’ opinion that the classification methods using borehole information should be removed from the Standard entirely.

There may be special circumstances where a borehole may be useful, such as to identity rock at very deep soil sites or where there are deep deposits of gravel. Even in those cases, the most useful purpose of a borehole would be to provide a hole for a downhole seismic test, rather than be used in itself for the purposes of site classification. It is often suggested that a borehole should be done to verify the findings of a CPT or SCPT, but there is little point in this as borehole information cannot reliably determine shear wave velocity and so provides a poor reference for comparison.

The in situ testing of shear wave velocity, the first of the three methods listed above, can be achieved by a variety of means, such as direct push downhole seismic, MASW, cross-hole seismic, borehole downhole seismic or downhole p-s suspension logging. Many of these methods require either a borehole to be drilled and/or significant post processing. Direct push downhole seismic, such as SCPT or seismic dilatometer (SDMT), is rapid and cost-effective in comparison to the other methods and does not require a borehole. The use of dual geophone modules (true-interval) greatly improves the accuracy of the test and cross-correlation software reduces post processing times. A SCPT combines the downhole seismic component with a conventional CPT, which allows an independent correlation to Vs to be made. Estimates of
Vs can also be made using the data from the DMT component of a SDMT, but the CPT provides a more continuous data set.

Consequently, the SCPT provides two independent estimates of Vs, which can be used to determine site period. By adding the HVSR method, a further independent estimate of site period can be obtained. It is the use of these methods (SCPT and HVSR) for estimating site period that is the topic of this paper.

2 HVSR

The horizontal to vertical spectral ratio method (HVSR), or Nakamura method, is a method of estimating the fundamental site period from ambient vibrations recorded passively at the ground surface. The method is described by Nakamura (1989). A more detailed analysis of the method is given in a European study named, SESAME (Acerra, et al. 2004).
The HVSR method uses the signals recorded from a three-sensor seismometer, comprising two horizonal sensors (North-South and East-West) and one vertical sensor. The recordings are made concurrently at a single station with the seismometer placed on the ground surface to record passive waves. The recording time at each station is usually between thirty minutes and one hour, although may need to be longer for very deep soil sites.

The ambient vibrations are effectively seismic waves forming a constant background noise made up, in general, of frequencies over 1 Hz from anthropogenic sources, and below 1 Hz from natural sources such as ocean waves. The waves of interest are likely to be a combination of surface waves (Rayleigh and Love waves) as well as body waves (compression and shear waves). At the resonant frequency of the soil deposit, these waves will tend to amplify in the horizontal direction and be attenuated in the vertical direction in their surface expression. By considering the ratio of the horizontal to the vertical amplitudes, the resonant frequency can be identified.

The signals from each of the three sensors are initially processed in parallel by splitting each component into matching time windows, usually of thirty seconds or one minute. This allows windows with unusable signals to be removed. The recorded signals in each window are split into their component frequencies using a Fourier transform algorithm. The results are smoothed using the method by Konno & Ohmachi (1998). The two horizontal components are averaged and then divided by the vertical. The resulting H/V ratios are plotted on frequency spectra for each time window. The mean of all the H/V ratios is made to provide a single averaged spectra line, along with lines indicating one standard deviation above and below the mean.

A peak in the H/V spectra indicates the resonant frequency of the site. The SESAME 2004 guidelines provide criteria for identification of a clear frequency peak to allow the user to assess the reliability of the indicated resonant frequency. Once the resonant frequency of the site is estimated, the site period can be determined by
(1)

where. T0 = fundamental site period, f0 = fundamental resonant frequency

Figure 1: Example of HVSR for site in South Auckland: (a) with all data; (b) with only mean and standard deviation lines shown

An example of a HVSR plot is given in Figure 1, below. This has been derived using the open source software, Geopsy (Wathelet et al. 2020). The data is from a site in South Auckland in Puketoka Formation soils with depth to rock of approximately 38 m. The graph shows a solid line that represents the mean of the data with dashed lines above and below representing one standard deviation either side of the mean. There is a distinct peak in the plot, which meets the SESAME 2004 criteria. The peak indicates a fundamental resonant frequency, f0 = 1.5 Hz. This corresponds to a fundamental site period, T0 = 0.67 s.

In some situations, there may be more than one clear peak at different frequencies. This would indicate significant impedance contrasts within the total soil mass above the rock surface. In that case it is the lowest frequency peak that represents the fundamental resonant frequency of the total soil mass. However, multi-peak HVSR plots may suggest complex ground conditions and it may be necessary to consider the effects of the various impedance contracts and how their related resonant frequencies affect the dynamic response of the site for design purposes. Knowledge of the geological setting is especially important for correct interpretation of the results. HVSR should not be used as a standalone method. It should be supported by existing ground information or used in combination with other testing methods, such as SCPT.

3 SCPT

3.1 Determining Vs from SCPT

The seismic cone penetrometer test (SCPT) utilises a conventional CPT probe coupled with a seismic module, which enables a downhole seismic test to be done in conjunction with a normal CPT. The test is performed by direct push from a CPT rig. The seismic module considered in this paper has two geophones spaced at 0.5 m apart and this is usually undertaken as a separate push to the CPT. The push is halted every 0.5 m depth to allow the seismic test to be carried out. The seismic test involves hitting a beam on the ground surface close to the CPT rods to generate a shear wave in the ground. At the instant that the beam is hit, the geophones begin recording and soon after a signal is recorded by the upper geophone and then by the lower geophone. The signals from each geophone are recorded and presented as two waves, which are offset by a short interval of time; the offset being the time for the wave to travel between the two sensors. Computer software is used to cross-correlate the two waves using curve-fitting algorithms to obtain the time difference between the two waves. Once the time difference is known, the shear wave velocity, Vs, over the depth interval between the sensors can be calculated. This specific method is described in more detail by Marchetti, et al. (2008). The advantage of this system is that it provides real time estimation of Vs as the test is being carried out on site. The test is repeated a few times, then the module is pushed to the next depth interval and the seismic testing repeated. This continues until the end of the sounding. The result is a shear wave velocity measurement of each 0.5 m interval over the full depth of the sounding. These tests have been conducted on many sites in Auckland in the Puketoka Formation, which is a geological unit comprising Pleistocene to Holoscene Age sedimentary deposits of clay, silts and sands. The resulting Vs with depth for three of these sites is illustrated in Figure 2 as the orange line in each plot.

Figure 2: Examples of Vs measured from downhole seismic and estimated from CPT correlations for three sites in Puketoka Formation soils in Auckland

It should be noted that the seismic component (S) and the CPT component of the SCPT are independent tests that can be done concurrently in the same push or done as separate pushes. The CPT component provides cone resistance, qc, sleeve friction, fs and pore pressure, u2, that can be correlated to various soil properties via empirical or semi-empirical correlations (e.g. Robertson 2009). There are many correlations that have been established for estimating Vs from CPT (e.g. Andrus, et al. 2007, Hegazy and Mayne 2006, Robertson 2009, Wair, et al. 2012). For this paper, we are considering the correlation developed by Robertson (2009), which is represented by Equation 2, below. This is also the equation that is utilised in the popular computer software program, CPeT-IT v3.0.3.2, by GeoLogismiki.

(2)

where αvs = 10(0.55 Ic + 1.68), Ic = soil behaviour index, qt = total cone resistance, σv = overburden stress.

The estimated Vs from the CPT data using Equation 2 is plotted in Figure 2 as the blue lines in the plots. By plotting both the measured Vs from the downhole seismic test and the estimated Vs from the CPT correlation, a comparison between the results can be made. This can provide validation to the particular correlation that is used or allows a site-specific correlation to be developed. If the measured and estimated Vs values are in agreement, as they generally appear to be in the plots in Figure 2, then some level of confidence is provided. It is the Authors’ experience, that Vs estimated from CPT using Equation 2 compares reasonably well with Vs measured from downhole seismic testing in the Puketoka Formations soils.

A comprehensive study of empirical correlations to Vs from CPT was carried out in the Christchurch area using a large database of SCPT’s (Wotherspoon, et al 2019). That study compared a number of published correlations, including that represented by Equation 2 (Robertson 2009). In that study, the function form represented by the Robertson equation was found to be one of least applicable for the Christchurch dataset, which are mainly sandy soils. Correlation to the Auckland Puketoka soils has not been as comprehensively studied. The purpose of this paper is to provide a mechanism for using Vs for site period and subsoil classification. It is not intended to be a comprehensive validation of the Robertson equation. The Robertson equation (Equation 2) was chosen in this paper due to its easy of use in the CPeT-IT software. More experimental evidence is required, however, for the purposes of this paper, it would appear that Equation 2 provides a reasonable estimation in these soils.

3.2 Time averaged shear wave velocity Vsz

The average shear wave velocity can be calculated by
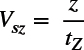(3)

where Vsz = time averaged shear wave velocity to depth z from the ground surface, and

(4)

where tz is the total time (s) for a shear wave to travel from the surface to depth z, Vsi is the shear wave velocity (m/s) over depth interval hi (m), nz is the number of depth intervals from the surface to depth z.

For the seismic component of the SCPT, each depth increment, h, will be equal to the interval depth; in this case, 0.5 m. There is potentially some error in the calculation of tz in this approach as the depth intervals in practice may not necessarily be perfectly aligned in sequence. In addition, any minor errors in the calculation of Vs at each interval may present a larger cumulative error. For the CPT estimated Vs values, the depth increment, hi, can be taken as the measuring interval of the CPT (e.g. 10 mm).

Figure 3: Plots of; (a) Vs ;(b) Vsz and; (c) T with depth for site in South Auckland

Figure 3(a) shows Vs with depth profiles from a SCPT on a site in South Auckland in Puketoka Formation soils. This is the same site as the HSVR example given in Figure 1, above. The measured Vs values are from the downhole seismic part of the test and the estimated Vs values are derived from the CPT data using Equation 2. The measured Vs and estimated Vs plots in Figure 3(a) do not compare overly favourably, but they do follow the same general trend. The reason for the relatively poor correlation may, in part, be due to the highly layered and variable ground conditions at this site, which can make the downhole seismic testing more difficult to interpret. In addition, the seismic testing is over 0.5 m depth intervals, whereas the CPT correlations are made at each CPT depth measurement (every 10 mm) and so are less comparable in these soil conditions. It is also likely that empirical correlation from CPT is not perfect in some of these soil layers. In general, it would appear that the measured Vs values provide an averaged profile through those estimated from the CPT correlations.

Figure 3(b) shows the time averaged shear wave velocity, Vsz, plotted with depth from the same SCPT. Both those determined from measured and estimated Vs are plotted. These averaged Vsz plots show a better agreement than that suggested by the Vs plots, with the two Vsz lines coming together nicely.

Determining site period and subsoil class

The site period, T, can be estimated by four times the shear wave travel time through the soil from the surface to the underlying rock (NZS 1170.5:2004).

(5)

where tH = total shear wave travel time (s) from the ground surface to the underlying rock using Equation 4.
Alternatively, the site period can be calculated by

(6)

Where H = total depth of soil from the ground surface to the underlying rock, VsH = time averaged shear wave velocity at depth H.

Equation 6 can be presented as a plot with depth, as illustrated in Figure 3(c). The purpose of this plot is to show a trend with depth, but it is only the point at the underlying rock interface that provides the site period. The depth to the top of the rock as suggested by the CPT refusal is 38 m. At this depth, the CPT estimated curve in Figure 3(c) suggests a site period, T = 0.71 s. This is slightly higher than the 0.67 s estimate from the HVSR (see Figure 1). The downhole seismic testing stopped short at 33.5 m depth. By extrapolating the seismic curve in Figure 3(c) down to the rock depth, an estimate of site period, T = 0.69 s is obtained. The method for extrapolating the curve is explained further below.

We now have three independently derived estimates of site period from the same location. These are summarised in Table 1, below.

Table 1: Estimates of site period from the various methods.

There is reasonable agreement between the three methods considering the potential uncertainty in these methods and in the ground conditions. More weight would be put on the downhole seismic and HVSR methods, although the use of all three at the same location provides a level of confidence. It would be reasonable to choose a site period, T = 0.7 s for design purposes. This is greater than 0.6 s, so the site would be classified as Class D in accordance with NZS 1170.5.

3.4 Extrapolation of Vsz and T with depth

In some cases, a SCPT may refuse before reaching rock. This may be due to impenetrable material being encountered, e.g. gravel, or otherwise reaching the limit of the CPT sensors. Alternatively, there may be uncertainty that CPT refusal is indicating rock proper.

In those cases, it may be useful to extrapolate the Vsz and T curves. If the depth to rock is known from existing information, e.g. a borehole, then these curves can be extrapolated to that depth, thus allowing T to be estimated. If a HVSR test has also been done at the same location, the estimated T from that test can be used for comparison. In cases where the rock depth is not known, then the site period estimated from the HVSR test can help estimate the rock depth by the extrapolation of the T curve from SCPT.

The extrapolation of the curves is reasonable provided that a distinct trend can be seen in the curves and that the data is not extrapolated too far, say, no further than 50% beyond the bottom depth of the SCPT. If the SCPT has reached a significant depth and there is an obvious trend, then the average shear wave velocity, Vsz, is likely to continue to follow that same trend as changes in Vs below that depth will have little effect on the overall average; at least over a small additional depth and provided the shear wave velocity doesn’t change dramatically.

In the above example site in South Auckland, the downhole seismic test stopped about 5 m short of the rock. A clear trend can be seen in the plot and extrapolation over that relatively short distance would not seem unreasonable. In that case, the data correlated from the CPT continues to the rock depth and provides a guide for the potential extrapolation of the seismic data. From Figure 3(c), it can be seen that continuation of the orange downhole seismic line results in a value of T at the rock depth slightly less than that of the blue line that was estimated from the CPT.

To develop this extrapolation in a more quantitative manner, the Vsz with depth relationship can be estimated by a power function. This can be developed by plotting (Vsz)2 with depth and considering the straight-line portion of the graph as shown in Figure 4 below. This is using the data form the downhole seismic part of the SCPT for the South Auckland example site and is a site-specific function.

Figure 4: Development of relationship between Vsz and depth

This provides a site-specific function of Vsz with depth as
(7)

A relationship for T with depth can be determined by combining equations (6) and (7). The resulting interpolated plots with depth for Vsz and T are shown in Figure 5, below. This shows only the downhole seismic data, but similar relationships can be determined this way for the CPT estimated Vsz and T.

Figure 5: Interpolation and extrapolation of Vsz and T data

4 Conclusions

The combination of SCPT and HVSR methods provides a convenient means of determining site period and subsoil class, particularly where depth to rock is achievable with SCPT. The SCPT provides two independent estimates of Vs: one measured from the downhole seismic part (S); and, the other estimated from empirical correlations from CPT. If done in combination with HVSR, three independent estimates of site period can be obtained. This provides a level of confidence in the results and allows for cross-validation of the methods.

In the example site at South Auckland, the three methods showed reasonable agreement in site period estimation (within 3%). This methodology is likely to be appropriate for the Puketoka Formation soils in Auckland, but would be equally suitable for other soil sites where depth to rock is within 50 m depth of the ground surface.

The empirical correlation for Vs from CPT used in this paper (Robertson 2009) appears to provide a reasonable estimate of Vs in the Puketoka Formation soils. However, this should not be relied on alone. More comprehensive research in this formation is needed to confirm this correlation or to establish a more reliable correlation.

5 References

Acerra, C., Aguacil G., Anatasiadis, A., Atakan, K., Azzara, R., Bard, Y., Basili, R., Bertrand, E., Bettig, B., Blarel, F., …, Moreno, B. 2004. Guidelines for the implementation of the H/V spectural ratio technique on ambient vibrations measurements, processing and interpretation. SESAME. European research project. WP12-Deliverable D23.12.

Andrus, R., Mohanan, N., Piratheepan, P., Ellis, B., Holzer, T. 2007. Predicting shear-wave velocity from cone penetration resistance. In: Proc. 4th International Conference on Earthquake Geotechnical Engineering. Thessaloniki, Greece, June 25-28, Paper No. 1454.

Hegazy, Y. & Mayne, P. 2006. A global statistical correlation between shear wave velocity and cone penetration data. In: Puppala, A., Fratta, D., Alshibli, K., Pamukcu, S. editors. Proc. of GeoShanghai, Site and Geomaterial Characterization (GSP 149). ASCE, Reston, VA; p. 243–8.

Konno, K. & Ohmachi, T. 1998. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor, Bull. Seismol. Soc. Am. 88, no. 1, 228–241.

Larkin, T. & van Houtte C. 2014. Determination of Site Period for NZS1170.5:2004. Bulletin of the New Zealand Society for Earthquake Engineering, Vol. 47, No. 1, March 2014.
Marchetti, D., Marchetti, S., Monaco, P., Totani, G. 2008. Experience with Seismic Dilatometer in Various Soil Types. Proc. Intnl. Site Characterization ISC’3, Taipei, Taiwan.
Nakamura, Y. 1989. Method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Quarterly Report of RTRI (Railway Technical Research Institute). Japan, 30(1):25-33.

Robertson, P. 2009. Interpretation of cone penetration tests – a unified approach. Canadian Geotechnical Journal 2009;46(11):1337–55.

Standards New Zealand. 2004. NZS1170.5 Eathquake Actions – New Zealand, Wellington, New Zealand.

Wair, B., DeJong, J., Shantz, T. 2012. Guidelines for Estimation of Shear Wave Velocity Profiles. Pacific Earthquake Engineering Research Center, University of California, Berkeley: PEER Report No. 2012/08.

Wathelet, M., Chatelain, J.-L., Cornou, C., Di Giulio, G., Guillier, B., Ohrnberger, M. and Savvaidis, A. (2020). Geopsy: A User-Friendly Open-Source Tool Set for Ambient Vibration Processing. Seismological Research Letters, doi: 10.1785/0220190360

Wotherspoon, L., Cubrinovksi, M., McGann, C., Bradley, B., Taylor, M. 2019. Development of an empirical correlation for predicting shear wave velocity of Christchurch soils from cone penetration test data. NZ Geomechanics News, Issue 97 – June 2019.